Ed25519 HD Key Derivation
Ed25519 and BIP-32、SLIP-10
先说结论,通常情况下,Ed25519 曲线是不能像 secp256k1 曲线一样直接使用 BIP-32 进行私钥派生的,因为这会导致私钥派生父私钥的必然泄露,破坏签名的安全模型,最终导致签名私钥被泄露。
所以针对 Ed25519 有了更加安全的规范,SLIP-10。其要求 Ed25519 永远只能使用 Hardened 派生(硬化派生):
- 不使用
child_pub = parent_pub + ... - 不允许父公钥推到子私钥
- 不允许从子私钥 + parent_pub 恢复 parent_priv
核心是因为 Ed25519 秘钥结构不支持可加性子密钥:
- 因为 Ed25519 的私钥是
hash(clamp(seed)) - BIP32 的加法公式不适用
- Ed25519 的 deterministic 特性会导致直接泄露父私钥
生成子密钥(统一硬化)Hardened 派生过程:
master_key, master_chain_code = HMAC-SHA512("ed25519 seed", seed)
Left 32 bytes -> key material
Right 32 bytes -> chain code
child_data = 0x00 || parent_key || index (big-endian 表示)
I = HMAC-SHA512(parent_chain_code, child_data)
进行切割:
child_key_material = I[0:32]
child_chain_code = I[32:64]
然后:
对于 Ed25519 曲线:child_key 需要 clamp
对于 secp256k1 曲线: child_key = child_key_material mod n
所以,ECDSA 的私钥 k 属于 [1, n-1] 的一个整数,而 Ed25519 的私钥则不是:
seed = 32 bytes random
h = SHA512(seed)
private_scalar = clamp(h[0:32])
public_key = private_scalar * B
clamp 将强制修改某些位:
h[0] &= 248 # 清除最低 3 bit
h[31] &= 63 # 清除最高 2 bit
h[31] |= 64 # 设置 bit 6
结果就是某些 bit 永远为 0, 某些永远为 1,私钥的分布是不均匀的,不满足完整的整数域。
sign safe
重点来了,如果我们强行在 Ed25519 上使用 BIP-32 派生,这会破坏私钥的 clamp 结构,将直接导致私钥的泄露。让我们先了解下 Ed 25519 的签名算法:
Ed 25519 的私钥通常是一个 32 bytes 的 seed
- 计算:
h = SHA512(seed) - 前 32 bytes
h[0:32]做 clamp 得到标量a(private_scalar) - 后 32 bytes
h[32:64]作为一个隐藏前缀prefix用于生成nonce
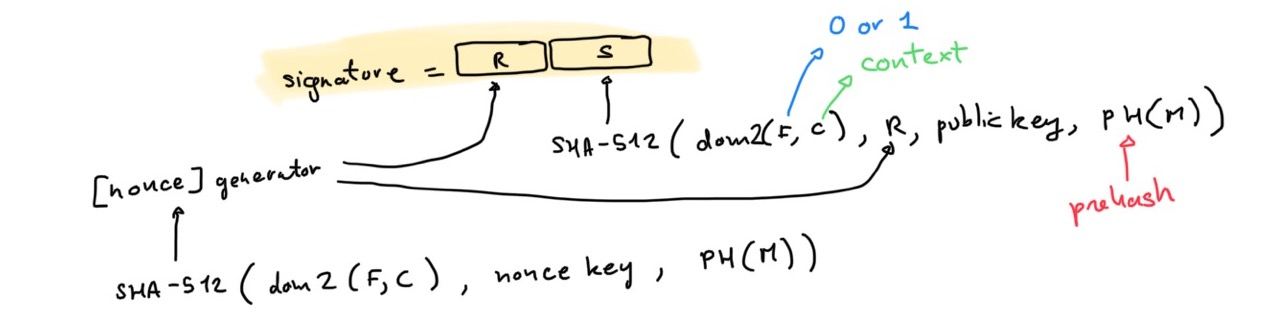
签名时,给定消息 M :
生成 nonce:
r = SHA5132(prefix || M) r_scalar = r mod L # L 为曲线 order计算公钥:
A = a * B计算 R 点:
R = r_scalar * B计算挑战:
k = SHA512(encode(R) || encode(A) || M) mod L计算签名:
S = r_scalar + k * a (mod L)
签名结果就是 (R, S)
关键点:
nonce r_scalar完全取决于prefix和message- 而
prefix是由seed的后半部分决定的,跟a有着紧密关系 - 这使得 nonce 不可预测,不可重用,不可控制
这套 nonce 的计算保证了 nonce 的高熵、不可预测,而且还不依赖于运行时 RNG。
但是,如果我们强行使用 BIP32 做私钥派生,如下:
a_child = a_parent + delta
那么直接使用两个签名 (R, S1) (R, S2) 便可直接推导出私钥 a.